13.03
4 клас
«Розв’язування задач на рух»
Тема. Повторення та закріплення вивченого матеріалу. Підготовка до контрольної роботи.
Мета. Тренувати здатність дітей до дій з багатоцифровими та змішаними числами, до розв’язання текстових задач і рівнянь вивчених видів.
Обладнання: індивідуальні картки з завданнями, опорні схеми, таблиці.
На дошці праворуч прикріплені в хаотичному порядку різнокольорові геометричні фігури з надрукованими буквами (в, р, а, с, т, р, м, п, о, р, т). Ліворуч – такі ж фігури з надрукованими натуральними та змішаними числами. Завдання полягає в тому, щоб розташувати фігури на координатній прямій у відповідному порядку(зайві фігури не використовувати) і скласти слово ,,транспортир,,.
І.Самовизначення до діяльності.
- Як називається команда ерудитів нашого класу?
- Допитливі.
- А який девіз команди?
- Ми допитливі малята, хочемо про все ми знати.
- А чи можу я стверджувати, що всі ви допитливі?
- То чи хочуть мої допитливі малята дізнатись, яке слово зашифроване на дошці і що воно означає?
- Чи можемо ми це зробити?
- Чи вірите ви в свої сили?
ІІ. Актуалізація знань.
1) Отже, щоб розшифрувати дане слово, потрібно розмістити деякі геометричні фігури в певному порядку на координатному промені. Перша позначка (червоний кружечок) стоїть на координаті 24. Як ви думаєте,чому?
- В класі 24 учні.
- Знайдіть на аркушах завдання з такою ж позначкою.
ІІІ. Повторення та закріплення вивченого
- 1) Знайти об’єднання та переріз множин.
П рочитай подвійну нерівність 15
рочитай подвійну нерівність 15  . Знайди множину А розв’язків цієї нерівності, кратних 4, і множину В її розв’язків, кратних 5. Потім знайди об’єднання і переріз множин А і В та побудуй діаграму Венна.
. Знайди множину А розв’язків цієї нерівності, кратних 4, і множину В її розв’язків, кратних 5. Потім знайди об’єднання і переріз множин А і В та побудуй діаграму Венна.
 рочитай подвійну нерівність 15
рочитай подвійну нерівність 15 - Яке число належить обом множинам?
- Число 20.
2) Знаходимо геометричну фігуру з таким числом (зелений трикутник) і розміщуємо її на координатному промені. На аркушах працюємо над завданням з такою ж позначкою.
- Бліц-турнір.
Б ліц-турнір
ліц-турнір
 ліц-турнір
ліц-турнір
а) У Мишка було a цукерок .  своїх цукерок він з’їв. Скільки цукерок у Мишка залишилось?
своїх цукерок він з’їв. Скільки цукерок у Мишка залишилось?
б) Женя склала k частівок, а Оленка – у 4 рази менше. Скільки всього частівок склали дівчата?
в) Оксанка купила 4 шпильки по m коп. за штуку і люстерко по n коп.. Скільки грошей у неї залишилось, якщо всього в неї було c копійок.
- Скільки виразів ми склали?
- 3.
3) Розміщуємо геометричну фігуру з таким числом (зелений кружечок) на координатному промені і виконуємо завдання з такою ж позначкою.
З адача
адача
 адача
адача
Турист повинен пройти за чотири дні 76 км. За перший день він подолав 25 км, за другий – на 5 км менше,ніж за перший, а за третій день – у 3 рази менше, ніж за 1 і 2 дні разом. Скільки кілометрів пройшов турист за четвертий день?
Завдання полягає в тому, щоб розв’язати задачу, склавши вираз.
- Скільки кілометрів мав пройти турист за третій день?
- 16.
- 4) Розмістіть фігуру з числом 16 (червоний трикутник) на промені і розв’яжіть наступне завдання (виконати обчислення за алгоритмом).
- Назвати найменше отримане число.
Обчислити за алгоритмом
| a | 1 | 1 | 2 | 4 | ||
| x |

- 


так




<1


+2 
- 





-
 .
. - 5) Знайдіть місце розташування наступної геометричної фігури (жовтий трикутник) на числовому промені та виконайте завдання з такою ж позначкою (порівняти дроби).
П орівняти дроби:
орівняти дроби:
 орівняти дроби:
орівняти дроби:- Скільки виконали порівнянь?
- 8.
- 6) Фігуру з числом 8 (синій квадрат) розміщуємо на координатному промені та виконуємо завдання (вибрати розв’язки нерівностей, записати числа з відповідними буквами в порядку зростання).
І з чисел, записаних праворуч від нерівностей, вибери ті, які є її розв’язками. Решту чисел закресли. Якщо завдання виконано правильно, то літери, які залишились, дадуть змогу визначити наступне завдання.
з чисел, записаних праворуч від нерівностей, вибери ті, які є її розв’язками. Решту чисел закресли. Якщо завдання виконано правильно, то літери, які залишились, дадуть змогу визначити наступне завдання.
 з чисел, записаних праворуч від нерівностей, вибери ті, які є її розв’язками. Решту чисел закресли. Якщо завдання виконано правильно, то літери, які залишились, дадуть змогу визначити наступне завдання.
з чисел, записаних праворуч від нерівностей, вибери ті, які є її розв’язками. Решту чисел закресли. Якщо завдання виконано правильно, то літери, які залишились, дадуть змогу визначити наступне завдання.| 5 |
| 4 |
| х=5 с | х=6 и | х=6 | х=5 |
| у= | у= | у=2 | у=3 |
| z=4 | z=4 | z=6 | z=5 и |
- 7) Утворене слово,, чотири,, вказує на наступний крок в нашій роботі (червоний квадрат). Самостійно знаходимо корені рівнянь (6
 ).
).
Р івняння
івняння
 івняння
івняння
22  - (y + 3
- (y + 3  )=5
)=5  + 6
+ 6  (x – 2
(x – 2  )∙60=240
)∙60=240
- 8) Розміщуємо синій кружечок з даним числом на координатному промені і відновлюємо ланцюжок обчислень.
- 9) Останнє число (11) є підказкою до вибору наступного завдання (синій трикутник):встановити істинність висловлювання.
В становити істинність висловлювання:
становити істинність висловлювання:
 становити істинність висловлювання:
становити істинність висловлювання:- Щоб встановити істинність висловлювання, потрібно скласти програму дій і знайти значення числівника.
-
 1 – хибне, тому що
1 – хибне, тому що  =15.
=15. -
 Жовтий квадрат з числом 15 розміщуємо на промені і виконуємо наступне завдання з такою ж позначкою.
Жовтий квадрат з числом 15 розміщуємо на промені і виконуємо наступне завдання з такою ж позначкою. -

Задача
І з пунктів А і В, відстань між якими 270км, одночасно в одному напрямку виїхали два поїзди. Швидкість першого поїзда дорівнює 80 км/год, а швидкість другого поїзда, який їде навздогін, 110км/год. Через який час вони зустрінуться?
з пунктів А і В, відстань між якими 270км, одночасно в одному напрямку виїхали два поїзди. Швидкість першого поїзда дорівнює 80 км/год, а швидкість другого поїзда, який їде навздогін, 110км/год. Через який час вони зустрінуться?
 з пунктів А і В, відстань між якими 270км, одночасно в одному напрямку виїхали два поїзди. Швидкість першого поїзда дорівнює 80 км/год, а швидкість другого поїзда, який їде навздогін, 110км/год. Через який час вони зустрінуться?
з пунктів А і В, відстань між якими 270км, одночасно в одному напрямку виїхали два поїзди. Швидкість першого поїзда дорівнює 80 км/год, а швидкість другого поїзда, який їде навздогін, 110км/год. Через який час вони зустрінуться?-
 9 годин.
9 годин. -
 9 надруковано на зеленому квадраті (бліц-турнір).
9 надруковано на зеленому квадраті (бліц-турнір).
Б ліц-турнір
ліц-турнір
 ліц-турнір
ліц-турнір
m км/год
a км/год
k км/год
км/год
км/год
n км/год
?
а)












t зустр. = 3 год
t зустр. = 4 год
d4 -?
S
a км/год
c км/год
k км/год
m км/год
г)










t-?
t=2 год
?
-

- Розмістіть фігури з буквами відповідно до фігур з числами.
- Яке слово ми склали?
- Транспортир.
ІV. Рефлексія діяльності.
- Будь ласка, дізнайтесь про призначення даного приладу та історію його виникнення
ДРОБИ
Частина — це кожна з рівних частин, на які поділено ціле.
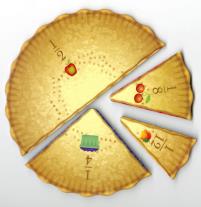
Половина пирога на малюнку — це друга частина; чверть — четверта частина. Для позначення частини використовують дворівневий запис із двох чисел, розділених горизонтальною лінією.
Наприклад, дванадцяту частину позначають 112 . Число під рискою показує кількість частин, на яку поділили ціле, а число над рискою — те, скільки взято частин.
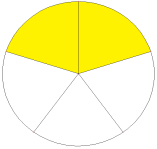
На малюнку коло розділено на п'ять частин, і дві з них зафарбовані. Кажуть, що зафарбована
частина — це дві п'ятих кола і записують як 25 . Це дробове число, або дріб 25 .
Число, записане над рискою дробу, називається чисельником дробу, а число, записане під рискою — знаменником дробу.
Знаменник показує, на скільки частин поділено ціле, а чисельник — скільки цих частин узято. Дріб є частиною або результатом додавання декількох частин.
Додавання рівних натуральних чисел можна замінити множенням числа на кількість цих чисел:
Те саме можна зробити і з сумою частин:
Для дробу з чисельником m і знаменником n правильною є рівність:
 https://youtu.be/0lGeQnjKAts задачі ДПА знаходження дробу від числа
https://youtu.be/0lGeQnjKAts задачі ДПА знаходження дробу від числа



Немає коментарів:
Дописати коментар